阅读札记——“5G信道的估计与均衡”
5G通信信道估计
一、MIMO——OFDM技术简介
MIMO：
多输入-多输出，即大规模天线阵列用于发送以及接收。
用基站端天线数量的扩展代替基站数量的扩展。
减少基站数量意味着多径效应的削弱，有利于减少小尺度衰减对信号传输的影响。
OFDM：
在传统的频分传输基础上，进一步节省频带资源，实现正交频分调制。
虽然OFDM各个子载波存在有频谱交叠的部分，但是由于是正交的，接收端仍能够解调信号并且可以高效的利用频谱。
MIMO在空间域上节省资源；OFDM调制在频域上节省资源。
二、mMIMO——Massive MIMO
MIMO的信道增益
多用户大规模MIMO，面向于多个用户接入，单个基站端配备有几十上百跟天线：
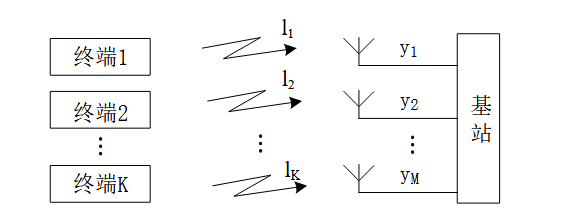
每个用户端只有一根天线，基站端配备有多根天线与用户相匹配。其中，第m根天线接收到来自第K个用户的信号Im,K在信道中的增益等于：
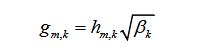
大尺度的衰减与小尺度的衰减相乘得到。其中，小尺度的衰减系数受天线的影响最大，可以认为是多个用户导致的用户间串扰（IUI-interUser interference）对于有M根天线阵列的基站来说，每根天线接收到K个用户传来的信号，将这
的信号组成矩阵，对应每个信号的信道增益就构成了信道矩阵。
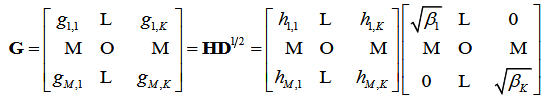
这也是CSI最终我们要得到的参数（矩阵）。
MIMO的信道分析
已知不同信道、不同信号的信道估计增益都不一样，这取决于大尺度衰弱叠加上小尺度干扰；因此为了增强信号的信噪比以及削弱用户间的干扰，我们可以采用最大合并比以及最大比发送实现，具体的思想就是根据CSI估计的信道衰减反馈在接收端或者发送端添加一个增益，以追求所有天线的信噪比之和最大。通常不同天线的增益满足：
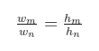
即增益与信道衰减成正比，与上述的描述相符。
那么我们如何通过CSI解得的信道矩阵求出最大比合并的权重？我们将矩阵写成列向量矩阵，每一列表示一个用户发出的信号被M根天线接受的信道衰减系数，属于小尺度衰减。我们对信道矩阵取模计算衰减可以得到下面式子：
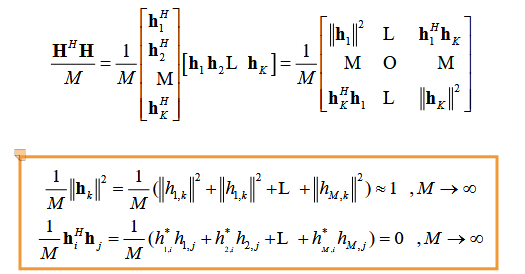
中间的展开式暂时不理解为什么等于这个结果，但是直接考虑到展开之前的部分，由于空间域的复杂性，我们可以假设不同天线的信道之间是互不相关的，由此我们就能知道一个信道的共轭转置乘上另一个信道可以理解求取为两个信道的相关性，因此可以近似于0；式子1的结果是因为当前信道和自己的相关性固然为1.这样我们只需要采用线性的处理方式即最大比合并就可以实现大规模MIMO中多个用户的传播。
MIMO优缺点
MIMO实现了在同时、同频进行多用户传播（利用波束空间复用），开发了空间域的资源利用，提高了容量。但是于此同时，随着用户数量大量增加，信道数量根据基站侧的天线数量尺度进行扩张，这也会导致导频资源的紧缺（世间真理，一件事物的宽裕会导致另一件事物的紧缺），导致导频污染。就像原本是一个8x8的象棋格，原本是错开的排列，当用户（列数）增加时，就会出现某一行有两个用户，这也就造成了导频污染。
OFDM调制
什么是OFDM调制
OFDM：正交频分复用，通过多载波调制（加载在不同的频段上）实现对频率选择性衰弱一定的抵抗，同时实现串行信号并行传输，提高速率且尽量节省频带资源。并行传输的优势还在于延长了单个符号的持续时间，假设我需要传输四个符号，每个符号持续0.25ns，那么一共传输1ns；如果我使用OFDM并行传输的话，使用4个子载波进行调制，那么在原来的传输时间1ns内我可以每个符号传输1ns并行传输，这样我单个符号的长度是原来的4倍，通过一些纠错码可以更容易校验符号、纠错，提高系统对ISI的抵抗性。
OFDM实信号的调制表达式如下：
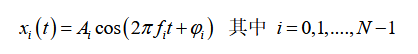
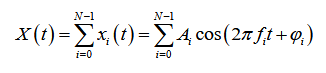
N为子载波的个数。在接收端由于每个子载波在频域上是相互正交的，可以容易的通过相干解调分离出每一个子载波承载的信号，最后再并串转换就可以得到信道传输后的接收信号。当然实际的调制过程更加复杂，一个可能的框图如下：
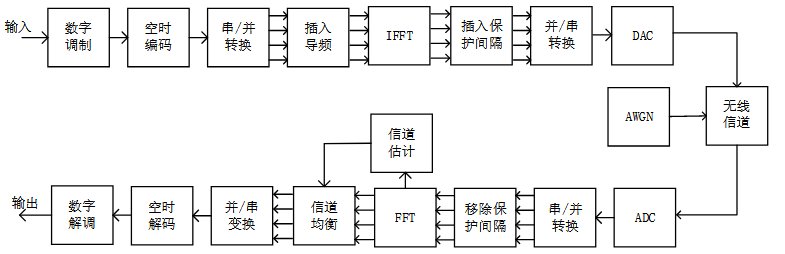
OFDM的技术特点
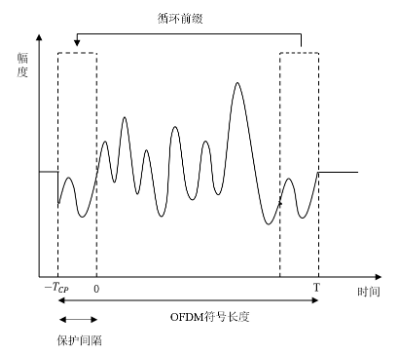
由于信道的不确定性，如多普勒频移导致的非正交性都会对OFDM传递的符号间产生严重的干扰；或者普遍存在的符号间干扰都会导致OFDM的正常传输，因此我们在传输的符号之间插入一段间隔称为保护间隔，通过牺牲一部分资源换取通信的稳定性。
在插入保护间隔的同时手动引入了时延，再加上多普勒频移导致子载波间不再是严格的正交，子载波信道之间会产生干扰，ICI即信道间干扰。于是添加了循环前缀，补全保护间隔的空缺，是不同信道的符号之间对齐，保持子载波之间的正交性，当然，这样也导致了资源的浪费，但是也能够减少复杂信号处理的开销。
信道估计
信道估计即是通过信道估计算法等数学分析手段研究时变无线信道的信道相关参数，这些参数对于接收端的数据恢复有很重要的作用。信道估计算法大致上可以分为三类，非盲估计、半盲估计和盲估计。这里的“盲”是指发送端的信号是否含有导频，所谓导频是一段接收方和发送方约定好的信号，通过观测导频发生的变化可以解出信道对当前信号的响应。因此我们一般使用非盲估计的方法。
传统信道估计算法
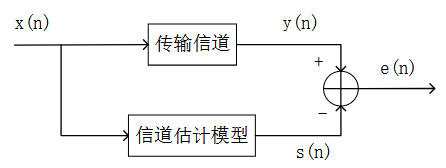
接收端的信号是传输信号通过信道的冲激响应后叠加一个加性高斯白噪声的结果，通过算法将接收信号还原接近发送信号，而估计与实际之间的误差就是衡量算法优越性的一个指标：
非盲估计是基于导频的信道估计算法，其中比较有代表性的有LS算法。即最小二乘法，其优点是复杂度低，易实现。信道模型如下
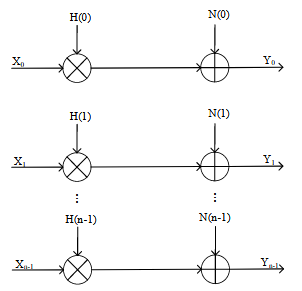
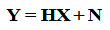
上述数学表达式是信号经过FFT后的频域表达，LS的估计目标是找到一个信道响应能够使HX即估计值与Y实际接收值之间的残差最小，数学表示如下：
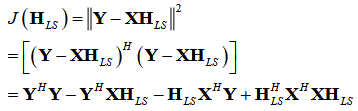
第一行就是求取两者的残差，矩阵运算也就等于共轭转置×原矩阵。最后的展开式是一个关于HLS的一个方程，我们想要让残差最小，也就是在方程的极小值处取值，因此我们对上式求偏导令等式两边为零，最终的结果是：
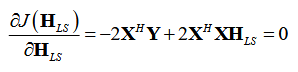
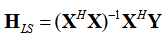
其中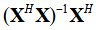
表示为X的伪逆矩阵。对LS算法求一下均方误差可以得到：
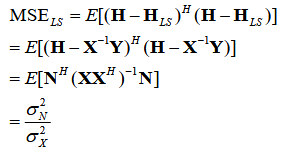
结果是信噪比（SNR）的倒数，也就是说当信道的信噪比越高，LS算法的估计效果越好，反过来也意味着LS算法易受噪声干扰。从模型的建立也可以看出，若忽略加性白噪声那一项，估计值就等于实际值。
由于LS算法对噪声的忽略，导致LS在实际的应用上估计误差较大，所以我们考虑另一种算法即MMSE算法。不像LS算法通过对导频信号的估计与原信号之间的差值来取得信道估计的最佳，MMSE直接对信道的冲激响应进行估计，然后通过信道响应的估计与真实信道响应之间的差值来取得最佳，这也就考虑到信道的多种特质（包括噪声）。
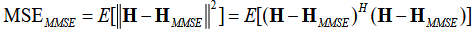
最小均方误差算法的思路就是实现信道估计结果与信道响应的真实值之间的均方误差达到最低值。我们假设一个矩阵M使得MY能够逼近发射信号X，令信道响应估计矩阵HMMSE为MY，均方差也就是
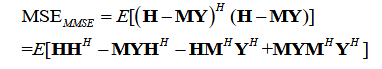
这是一个关于M矩阵的函数，我们想让均方差取得极小值也就是要令偏导为0。
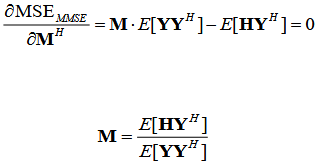
发现M矩阵是真实信道矩阵冲激响应与接收端信号的互相关矩阵乘上接收端信号自相关矩阵的逆。最后信道响应估计矩阵由等式HMMSE = MY得出
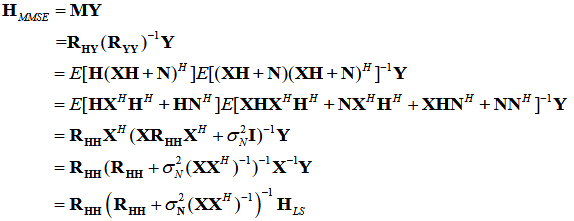
MMSE 信道估计算法相对于前面的 LS 算法,最大的改进之处在于消除噪声对信道估计的不良影响,能够实现更为精准的信道估计效果。但是我们从算法的思想中也可以发现，MMSE算法是基于真实信道的自相关矩阵实现的，算法要求信道的统计先验信息，而这往往需要很大的工作量，而且大量的矩阵运算也导致运算的复杂度增大以及算力的需求。
总结一下，上面两种算法对于信道估计在某些层面上都有较好的表现，LS算法是通过假定一个信道响应HLS，通过将导频通过假设的信道响应与接收端实际接收的导频之间的均方差来估计信道响应，这种假设忽略了信道中噪声的影响。而MMSE算法通过假设一个矩阵M，假定信道响应等于接收端的导频乘上矩阵M即MY，通过真实信道响应与估计的信道响应之间的均方差来估计信道响应，这种假设考虑到信道中的噪声提高了精度，但是需要先验条件即真是信道的自相关矩阵。
压缩感知
压缩感知基于信号的稀疏性。该技术的原理是:首先求取得到一个域,它可以实现将原始信号转换至此域后能展现出信号的稀疏性质,完成原始信号的稀疏变换;然后为变换得来的稀疏信号寻找合适的观测矩阵,形成较低维度的信号;最后以低采样的代价,应用重构算法把原来的信号估计出来,回到稀疏域进行处理。例如，信号通过无线信道到达基站的天线阵列，从到达的角度考虑，实际信号到达的角度很有限，在角度域上呈现出稀疏性。
如果信号本身不具有某些稀疏性，则利用某一正交基实现线性的稀疏转变：
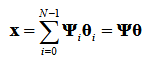
X是原始的N为信号向量，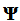
是稀疏变化矩阵，
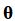是完成转变的稀疏信号。完成信号的稀疏转变后的第二部就是进行测量矩阵的设计问题，将上一步完成的稀疏信号与测量矩阵相乘的目的是将信号降维。（去除冗余的信息）
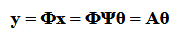
测量矩阵×稀疏变换矩阵得到了A即感知矩阵。原信号是一个N维的信号，而感知矩阵是一个M×N的矩阵，也就是说实现了降维，后续只需要借助M维信号就可以实现最终的原始信号的恢复。
