引言

在信号处理领域，参数估计是实现目标识别与定位的核心技术之一。经典论文《ESPRIT: Estimation of Signal Parameters via Rotational Invariance Techniques》提出了基于旋转不变性的超分辨率参数估计算法，而《Multiple Emitter Location and Signal Parameter Estimation》则进一步拓展了多信号源定位的理论框架。本文结合原始思想与最新改进算法，探讨3D建模下的参数估计方法。

ESPRIT算法核心思想

旋转不变性原理

ESPRIT算法的核心在于利用信号子空间的旋转不变性[[4]]。通过构建两个存在位移关系的传感器阵列，其接收信号满足：
$$
\mathbf{X}_2 = \mathbf{X}_1 \mathbf{\Phi}
$$
其中 $\mathbf{\Phi}$ 为包含信号到达角（DOA）信息的对角矩阵。通过对信号子空间进行奇异值分解（SVD），可直接从矩阵 $\mathbf{\Phi}$ 中提取信号参数[[4]]。

子空间分解

原始ESPRIT通过以下步骤实现参数估计：

  1. 构造阵列协方差矩阵并进行特征值分解；
  2. 分离信号子空间与噪声子空间；
  3. 利用子阵列间的平移关系求解旋转矩阵 $\mathbf{\Psi}$；
  4. 通过特征分解获得信号的波达方向（DOA）[[4]]。

MUSIC算法核心思想

核心思想

  1. 信号子空间与噪声子空间分离
    论文提出利用协方差矩阵特征值分解，将信号空间划分为信号子空间（由大特征值对应特征向量张成）和噪声子空间（由小特征值对应特征向量张成）。两者正交的特性成为参数估计的关键 [[2]][[9]]。

  2. 空间谱搜索
    通过构建如下MUSIC谱函数实现信号源定位：
    $$
    P_{\text{MUSIC}}(\theta) = \frac{1}{\mathbf{a}(\theta)^H \mathbf{E}_n \mathbf{E}_n^H \mathbf{a}(\theta)}
    $$
    其中 $\mathbf{E}_n$ 为噪声子空间，$\mathbf{a}(\theta)$ 为阵列流形向量。当 $\theta$ 扫描到真实信号方向时，分母趋近于零，谱峰位置即对应信号源方向 [[3]][[9]]。

扩展到三维空间下的估计

随着5G通感一体化和智能感知的发展，实际应用中对三维空间（方位角、俯仰角、距离等）参数的高精度估计提出了更高要求。传统MUSIC和ESPRIT算法主要针对二维（如仅估计方位角），而三维场景下需要对信号的多个空间参数进行联合估计。

三维ESPRIT算法

三维ESPRIT算法需要平面或者立体的天线阵列流形，这里我们以平面阵列流形为例，且相邻的天线之间的间距相等，即均匀平面天线（UPA）；

UPA

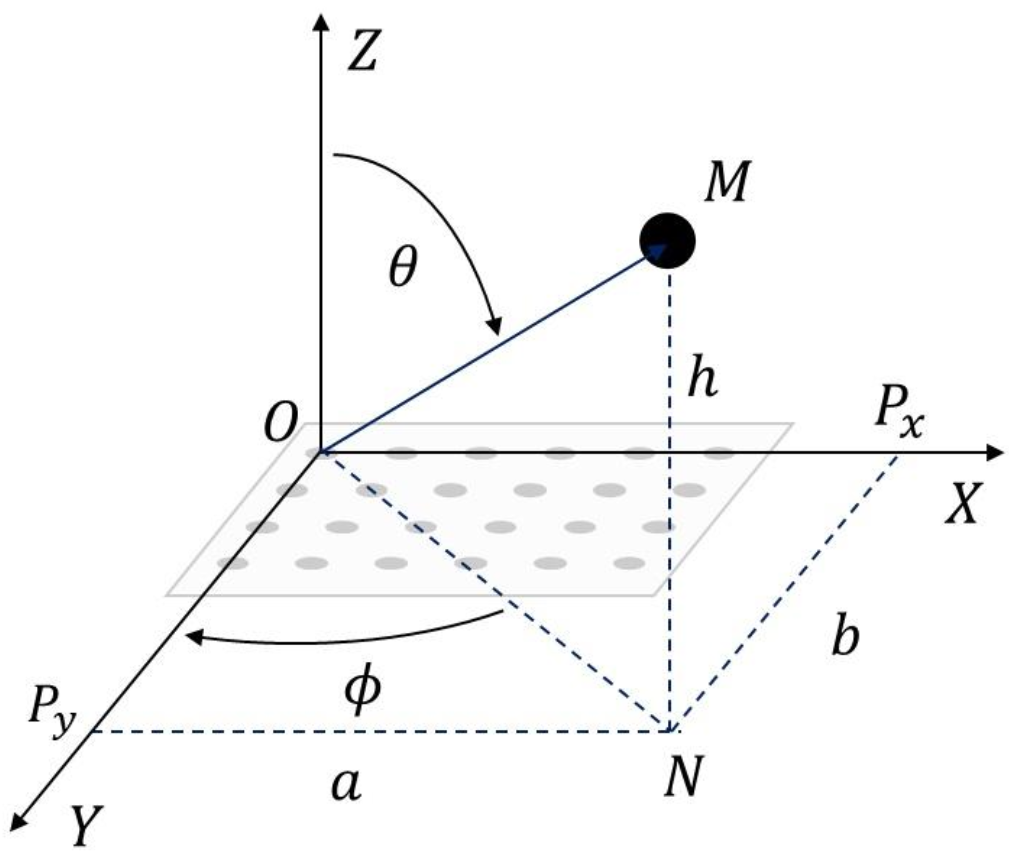
通过将信号的波达角分解为水平的方位角以及垂直的俯仰角，可以将信号到达不同天线的路程差通过天线间距$d$、方位角$\phi$以及俯仰角$\theta$联合表示：

$$
\Delta \lambda_{m,n} = d \left[ (m-1)\sin\theta\cos\phi + (n-1)\sin\theta\sin\phi \right]
$$

由于天线之间的间隔以及波达角导致的信号到达天线阵列所经历的时间不同，意味着信号到达不同天线的相位也不一样。由于是均匀分布的天线，我们可以推测，相邻天线之间的相位差是一个定值，因此可以通过选择天线对，然后由ESPRIT的算法得到旋转不变性，从而计算得到两个参数：$\sin\theta\cos\phi$ 以及 $\sin\theta\sin\phi$，之后便可以轻松的计算出我们需要的方位角$\phi$以及俯仰角$\theta$。

三维ESPRIT算法的难点

这里的难点在于，对接收到的信号做信道估计以及信道补偿一系列操作后得到的信道响应是所有天线阵列接收信道的叠加，从信道响应的形状上来说已经没有了天线阵列的形状信息，如何将信道响应$H$重新塑形则是一大难题。

对于如何获得信道响应，从感知的角度而言，将不同参数对应的导向矢量做克罗内克积便得到了信道响应：

$$
H = a_{aoa} \otimes a_{zoa}
$$

这里的$\otimes$代表克罗内克积（kronecker product），$a_{x}$表示为某个参数的导向矢量。这里得到的是理想信道响应，可以添加加性高斯白噪声以模仿实际的信道响应。

三维ESPRIT算法的具体实现

联合导向矢量的定义可以用x方向天线的导向矢量与y方向天线的导向矢量做克罗内克积得到

$$ A = A_{x} \otimes A_{y} $$

也可以通过直接的定义得到

1
2
3
4
5
6
7
8
9
10
11
12
# 构建二维阵列响应
def steering_vector_2d(az_deg, el_deg):
    #^ 角度值转弧度制
    az = np.radians(az_deg) # 方位角
    el = np.radians(el_deg) # 俯仰角
    kx = np.sin(el) * np.cos(az)
    ky = np.sin(el) * np.sin(az)
    a = np.zeros((Mx, My), dtype=complex)
    for m in range(Mx):
        for n in range(My):
            a[m, n] = np.exp(-1j * 2 * np.pi * (dx * m * kx + dy * n * ky) / wavelength)
    return a.flatten()

接收信号矩阵可以具体表现为

$$ X = AS + N $$

其中的$A_{M, K}$为接收矩阵的阵列响应，$S_{K, snapshots}$为$N$个信号源在接收天线的采样值，$N_{M, snapshots}$为噪声。

对接收信号直接做SVD，可以得到接收信号的协方差矩阵以及信号子空间和噪声子空间的基

1
2
3
4
# 协方差矩阵估计与SVD分解
R = X @ X.conj().T / snapshots  #^ [M, M]的协方差矩阵
U, _, _ = svd(R)
Us = U[:, :K]                   #^ [M, K]的信号子空间矩阵

其中特征向量的选择取决于信号源的个数，且形状为天线数X信号源数,对每一个特征向量进行重新塑形，具体思想为选择前$row - 1$天线阵元的响应和后$row - 1$天线阵元的响应，通过ESPRIT算法可以得到相位偏差，对应于x轴方向天线阵元之间的相位偏移$\sin\theta\cos\phi$。同理选择前$col - 1$天线阵元的响应和后$col - 1$天线阵元的响应可以计算出y轴方向天线阵元之间的相位偏移$\sin\theta\sin\phi$，从而得到波达角。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 构造移位子阵列索引
def shift_indices(dim_x, dim_y, axis):
    """
    函数作用: 先构建一个dim_x * dim_y的二维矩阵 索引从(0, 0)到(dim_x-1, dim_y-1)

    如果传入axis=0 则将行进行删除操作 然后按照行的顺序 顺次存取为一个一维的index 如0、1、2、...或者6、7、8、...
    如果传入axis=1 则将列进行删除操作 然后按照行的顺序 顺次存取为一个一维的index 如0、1、2、3、4、6、...或者1、2、3、4、5、7、...
    """
    if axis == 0:  # x 方向（垂直方向）移位
        rows = np.arange(dim_x - 1)
        idx1 = np.ravel_multi_index(np.meshgrid(rows, np.arange(dim_y), indexing='ij'), (dim_x, dim_y))
        idx2 = np.ravel_multi_index(np.meshgrid(rows + 1, np.arange(dim_y), indexing='ij'), (dim_x, dim_y))
    elif axis == 1:  # y 方向（水平方向）移位
        cols = np.arange(dim_y - 1)
        idx1 = np.ravel_multi_index(np.meshgrid(np.arange(dim_x), cols, indexing='ij'), (dim_x, dim_y))
        idx2 = np.ravel_multi_index(np.meshgrid(np.arange(dim_x), cols + 1, indexing='ij'), (dim_x, dim_y))
    return idx1.flatten(), idx2.flatten()

# 获取两个方向的子阵列
Ux1_idx, Ux2_idx = shift_indices(Mx, My, axis=0)
Uy1_idx, Uy2_idx = shift_indices(Mx, My, axis=1)

Ux1 = Us[Ux1_idx, :]
Ux2 = Us[Ux2_idx, :]
Uy1 = Us[Uy1_idx, :]
Uy2 = Us[Uy2_idx, :]

# 分别计算x方向和y方向的Psi矩阵
Psi_x = pinv(Ux1) @ Ux2
Psi_y = pinv(Uy1) @ Uy2

# 求解特征值并估计方向余弦
eigvals_x, _ = eig(Psi_x)
eigvals_y, _ = eig(Psi_y)

angles_x = np.angle(eigvals_x)
angles_y = np.angle(eigvals_y)

kx_est = angles_x * wavelength / (2 * np.pi * dx)
ky_est = angles_y * wavelength / (2 * np.pi * dy)

代码中定义的函数shift_indices中根据接收天线的形状定义每根天线的索引，x方向和y方向上分别取子阵列的阵元索引，具体可以看函数的解析。再通过索引选取特征向量中的元素，通过ESPRIT的算法便可以得到不同方向上天线阵元之间的信号相位差，再由相位差便可以轻松的得到波达角。

三维MUSIC算法

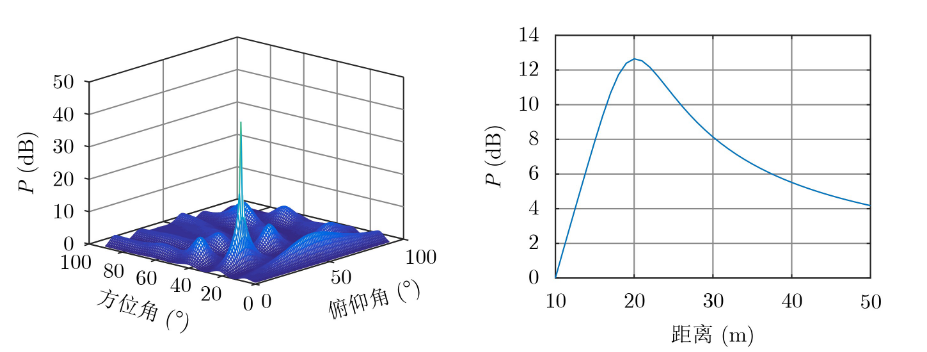
三维MUSIC算法通常基于三维阵列（如平面阵列或立体阵列），其核心思想与二维类似，但需要构造三维空间的阵列流形向量 $\mathbf{a}(\theta, \phi, r)$，并在三维参数空间内进行谱峰搜索：

$$
P_{\text{MUSIC}}(\theta, \phi, r) = \frac{1}{\mathbf{a}(\theta, \phi, r)^H \mathbf{E}_n \mathbf{E}_n^H \mathbf{a}(\theta, \phi, r)}
$$

其中，$\theta$ 为方位角，$\phi$ 为俯仰角，$r$ 可为距离或极化等参数。通过在三维参数空间内搜索谱峰，实现对信号源空间位置的精确估计。该方法分辨率高，但计算量大，常需结合降维或并行计算优化。

互素阵列流形——降维MUSIC算法

均匀平面阵列(Uniform Planar Array, UPA) 是一种经典模型,其相邻阵元间距均为半波长,该 模型在3维信源定位时精度较高,但在阵列口径较 大时,较高的结构复杂度限制了该模型的应用。为 了实现低复杂度的3维信源精确定位,本文提出 CLACS-SPA结构,其主要特征是将一列互素线阵 (Coprime Linear Array, CLA)沿着与之垂直的方 向按照相同的互素规律进行平移而得到 [[5]]。

互素面阵

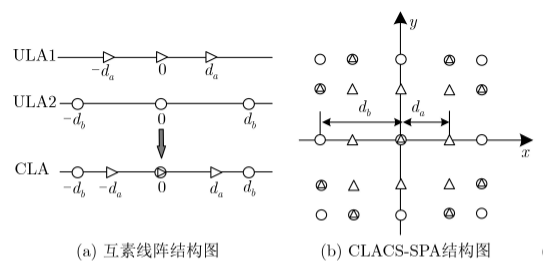
图中左图$ULA1$为间隔为$a$的均匀线阵，$ULA2$为间隔为$b$的均匀线阵，将两个线阵拼接在一起且间隔互为素数则得到了互素线阵；有图中将这样的互素线阵在垂直的方向上拼接就得到了互素面阵。

对于这样的互素面阵，信源到不同天线之间相位差可以如下面这样表示：

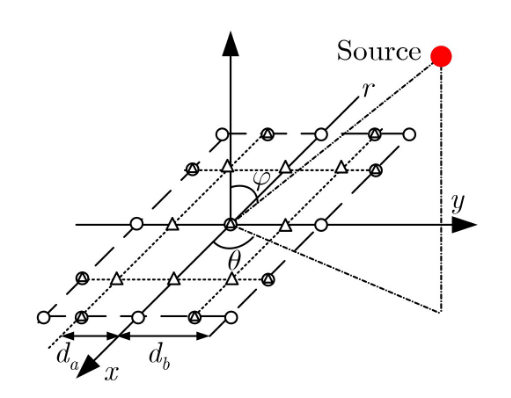
相位差计算

分别从x轴方向和y轴方向计算相邻两个天线之间的信源波程差可以得到

$$
\begin{align}
\Delta_{x,k} &= \sqrt{r^2 + l_{x,k}^2 - 2l_{x,k}r \sin\varphi \cos\theta} - r \tag{2} \
\Delta_{y,k} &= \sqrt{r^2 + l_{y,k}^2 - 2l_{y,k}r \sin\varphi \sin\theta} - r \tag{3}
\end{align}
$$

有前面我们可以清楚的知道，波程差一定程度上等价于相位差，而波程差又取决于波达角以及距离（飞行时间）。所以，相位差是由三维参数共同决定的，这也就是说通过MUSIC算法遍历三维空间计算量十分庞大，那么有没有什么办法减少计算呢？

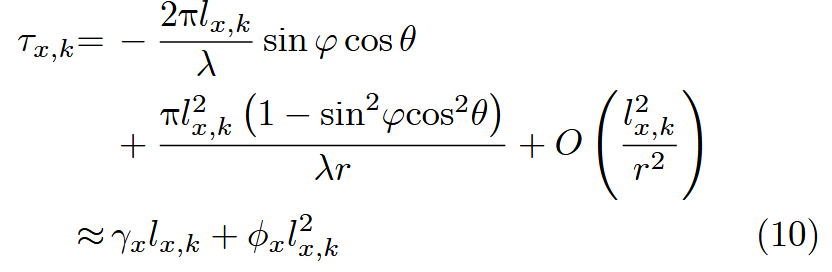
泰勒展开降维

上述式子展示了将x或者y方向的波程差通过泰勒公式展开，对高阶项直接舍去便得到了
$\gamma_x = -\frac{2\pi \sin\varphi \cos\theta}{\lambda}, \quad
\phi_x = \pi \left(1 - \frac{\sin^2\varphi \cos^2\theta}{\lambda r}\right); \quad$

其中的$\gamma_x$只跟波达角有关，在求出波达角后$\phi_x$就只跟距离有关，如此便将一个三维的搜索转换为二维的搜索加上一维的搜索，大大降低了计算复杂度。

互素阵列流形MUSIC算法具体实现

首先是根据泰勒展开后的第一项构建搜索导向矢量$\hat{A}_{x}$，在一定的角度范围内遍历$\theta, \phi$并计算谱值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 泰勒近似方向导向项构造函数
def xi(l, gamma):
    return np.exp(1j * gamma * l)

#^ 第一阶段：二维角度搜索 泰勒展开后的零次项作为预测的导向矢量估计ZOA、AOA
for i, phi in enumerate(phi_scan):
    for j, theta in enumerate(theta_scan):
        #^ 泰勒展开的零次项
        gamma_x = -k * np.sin(phi) * np.cos(theta)
        gamma_y = -k * np.sin(phi) * np.sin(theta)
        
        xi_x = xi(Lx, gamma_x)  #^ [9, 1] 横向的天线响应
        xi_y = xi(Ly, gamma_y)  #^ [9, 1] 纵向的天线响应
        xi_xy = np.kron(xi_x, xi_y).reshape(-1, 1)          #^ [81, 1] 降维后x方向的导向搜索矢量
        
        #^ 遍历角度 构建导向矢量 计算与噪声子空间的距离 
        psi = xi_xy.conj().T @ Un @ Un.conj().T @ xi_xy     
        Pmap[i, j] = 1 / np.real(psi)                       #^ 计算谱值 1/psi 最大值为波达角

找到最大的谱值对应的波达角，将波达角带入到第二项中，就变成了距离$r$的单一求解，构建搜索导向矢量并在给定的范围内搜索谱值的最大值，具体如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def upsilon(l, phi_term):
    return np.exp(1j * phi_term * l**2)

#^ 泰勒展开的一次项 带入估计的波达角
for r in r_scan:
    phi_x = np.pi / (lam * r) * (1 - np.sin(phi_est)**2 * np.cos(theta_est)**2)
    phi_y = np.pi / (lam * r) * (1 - np.sin(phi_est)**2 * np.sin(theta_est)**2)
    
    upsilon_x = upsilon(Lx, phi_x)
    upsilon_y = upsilon(Ly, phi_y)
    upsilon_xy = np.kron(upsilon_x, upsilon_y).reshape(-1, 1)
    
    # 需要带上零次项进行估计
    xi_x = xi(Lx, -2 * np.pi / lam * np.sin(phi_est) * np.cos(theta_est))
    xi_y = xi(Ly, -2 * np.pi / lam * np.sin(phi_est) * np.sin(theta_est))
    xi_xy = np.kron(xi_x, xi_y).reshape(-1, 1)
    
    # 指数相乘等于相位相加 对应泰勒展开的项
    A_est = xi_xy * upsilon_xy
    pseudospectrum = 1 / np.real((A_est.conj().T @ Un @ Un.conj().T @ A_est))
    P_r.append(pseudospectrum[0][0])

最后便可以在保持高精度的前提下简化计算复杂度提高速度

参数估计

总结

从最初的经典ESPRIT和MUSIC算法，到近年来面向三维建模和5G通感一体化的多维参数估计算法，参数估计技术正不断向高精度、高分辨率和强鲁棒性方向演进。随着阵列结构的创新（如互素阵、稀疏阵列）和信号处理手段的提升（如空间平滑、极化信息融合、降维搜索等），改进算法不仅在低信噪比、强干扰等复杂环境下展现出更优的性能，还显著降低了计算复杂度，提升了实时性和工程可用性。这些进步为5G通感一体化、智能感知、无人系统等前沿应用提供了坚实的技术基础和广阔的发展空间[[1]][[2]][[4]]。

参考资料：
[[1]] 基于改进3D-ESPRIT的GTD模型参数估计
[[2]] 三维GTD模型参数估计的改进算法
[[3]] CN111781573A 专利文档
[[4]] TLS-ESPRIT改进空间平滑算法
[[5]] 基于稀疏面阵的低复杂度三维信源定位算法