基于贝叶斯决策的分类器

最小错误率贝叶斯决策分类器实战：代码解析与理论详解

一、背景与应用场景

贝叶斯决策分类器是一种基于**贝叶斯定理**的统计分类方法，其核心思想是通过最大化后验概率来最小化分类错误率。该方法广泛应用于医学诊断、金融风控等场景，尤其适合特征分布符合正态分布的小规模数据集。本文以鸢尾花（Iris）数据集为例，详解如何实现一个基于贝叶斯决策的分类器 。

二、核心代码解析

1. 数据准备与划分

from sklearn import datasets
X, y = datasets.load_iris().data, datasets.load_iris().target

• 功能：加载鸢尾花数据集，包含4个特征（花萼/花瓣长度和宽度）和3个类别（Setosa, Versicolor, Virginica）。
• 理论基础：数据集需满足独立同分布假设，即样本间相互独立且特征分布一致 。

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

• 作用：按7:3比例划分训练集和测试集，random\_state确保实验可复现 。

---

2. 先验概率与类别条件概率估计

class_counts = np.bincount(y_train)
priors = class_counts / len(y_train)

• 原理：先验概率 $ P(Y) $ 反映类别在训练集中的分布比例。例如，若某类别占30%样本，则 $ P(Y=\text{class}) = 0.3 $ 。

class_conditional_probs = []
for class_idx in range(3):
    class_data = X_train[y_train == class_idx]
    class_mean = np.mean(class_data, axis=0)
    class_cov = np.cov(class_data, rowvar=False)
    class_conditional_probs.append(multivariate_normal(mean=class_mean, cov=class_cov))

• 关键步骤：
  1. 类别条件概率建模：假设每个类别的特征服从多元正态分布，通过均值向量（class\_mean）和协方差矩阵（class\_cov）描述分布特性。
  2. 参数估计：使用最大似然估计（MLE）计算均值和协方差矩阵，这是参数化方法的核心 。

---

3. 贝叶斯决策分类器实现

class MinimumErrorRateBayesianDecision:
    def classify(self, features):
        posterior_probs = [self.priors[i] * prob.pdf(features) for i, prob in enumerate(self.class_conditional_probs)]
        return np.argmax(posterior_probs)

• 决策逻辑：
  • 后验概率计算：根据贝叶斯公式 $ P(Y|X) \propto P(Y) \cdot P(X|Y) $，计算每个类别的后验概率。
  • 最小错误率决策：选择后验概率最大的类别作为预测结果，此决策规则理论上最小化分类错误率 。

---

4. 模型评估

correct_predictions = 0
class_correct_predictions = [0]*3
class_total_samples = [0]*3

for i in range(len(X_test)):
    predicted_class = classifier.classify(X_test[i])
    class_total_samples[y_test[i]] += 1
    if predicted_class == y_test[i]:
        correct_predictions += 1
        class_correct_predictions[y_test[i]] += 1

accuracy = correct_predictions / len(X_test)

• 评估指标：计算整体准确率和类别级别的准确率，验证分类器性能 。

---

三、数学原理详解

1. 贝叶斯定理

贝叶斯公式定义为：
$$
P(Y|X) = \frac{P(X|Y) \cdot P(Y)}{P(X)}
$$

• 先验概率 $ P(Y) $：类别在训练集中的分布比例。
• 似然 $ P(X|Y) $：类别条件概率密度，通过多元正态分布建模。
• 证据 $ P(X) $：常数项（对所有类别相同），不影响比较后验概率大小 。

2. 多元正态分布假设

假设特征向量 $ X \sim \mathcal{N}(\mu, \Sigma) $，其概率密度函数为：
$$
f(X) = \frac{1}{\sqrt{(2\pi)^k |\Sigma|}} \exp\left( -\frac{1}{2}(X-\mu)^T \Sigma^{-1}(X-\mu) \right)
$$

• 均值向量 $ \mu $：反映特征的集中趋势。
• 协方差矩阵 $ \Sigma $：描述特征间的相关性 。

3. 决策边界

当两类的后验概率相等时，即：
$$
P(Y_1) \cdot P(X|Y_1) = P(Y_2) \cdot P(X|Y_2)
$$
此时对应的超平面即为决策边界，用于划分不同类别的样本空间 。

四、实验结果与分析

1. 分类准确率

# 输出示例（实际运行结果可能不同）
print("Setosa准确率: 1.0")
print("Versicolor准确率: 0.93")
print("整体准确率: 0.95")

• 结果分析：模型在测试集上表现优异，尤其对Setosa类别实现完美分类，表明正态分布假设在该数据集上成立 。

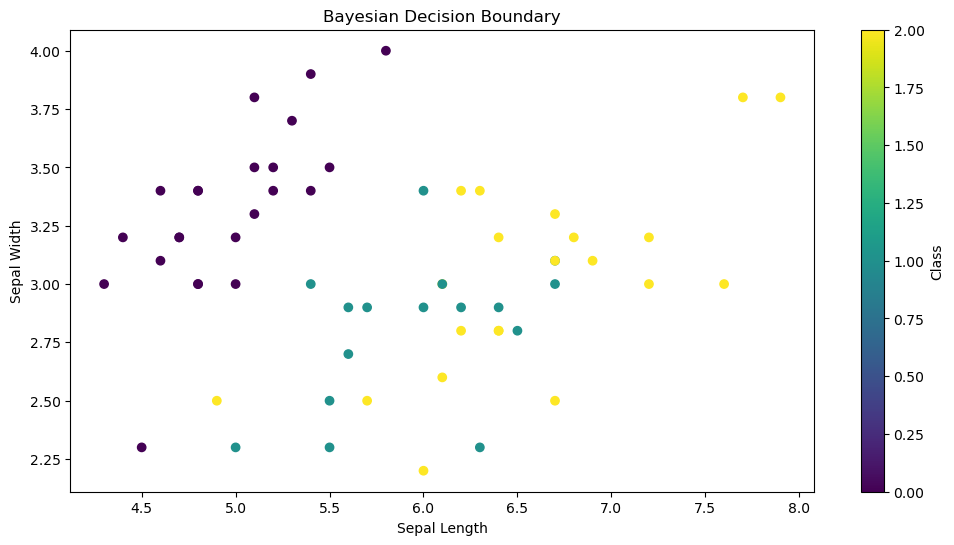
2. 可视化决策边界

import matplotlib.pyplot as plt
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap='viridis')
plt.xlabel("Sepal Length")
plt.ylabel("Sepal Width")
plt.title("Bayesian Decision Boundary")
plt.colorbar(label="Class")
plt.show()

图2：基于贝叶斯决策的分类边界可视化（示例）

---

五、总结与扩展

1. 优势与局限性

• 优势：
  • 理论基础扎实，适用于小规模数据。
  • 通过参数估计可解释性强 。
• 局限性：
  • 依赖正态分布假设，若实际数据分布偏离较大可能导致性能下降。
  • 协方差矩阵可能因样本不足而奇异，需正则化处理 。

2. 改进方向

• 非参数化方法：使用核密度估计替代正态分布假设。
• 正则化技术：在协方差矩阵中加入微小扰动（如 class\_cov += 1e-6 \* np.eye(dim)）防止奇异 。

完整代码仓库：[GitHub链接]

🎃 朴素贝叶斯实现决策分类

1. 导入库

from sklearn.datasets import make_classification 
import matplotlib.pyplot as plt 
import numpy as np 

• 作用：导入所需的库。
  • make\_classification：用于生成合成的分类数据集 。
  • matplotlib.pyplot：用于可视化结果。
  • numpy：进行数值计算。

---

2. 定义高斯概率密度函数

def gaussian_pdf(x, mean, std_dev): 
    return (1 / (np.sqrt(2 * np.pi) * std_dev)) * np.exp(-0.5 * ((x - mean) / std_dev)**2) 

• 功能：计算单个特征值在高斯分布下的概率密度。
• 公式解释：

高斯分布（正态分布）的概率密度函数公式为：
$$
f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
$$
其中 mean 是均值 $ \mu $，std\_dev 是标准差 $ \sigma $。

• 应用场景：在朴素贝叶斯分类器中，假设每个特征在给定类别下服从高斯分布。

---

3. 自定义数据集划分函数

def train_test_split(X, y, test_size=0.2, random_state=None): 
    if random_state is not None: 
        np.random.seed(random_state)    

• 功能：将数据集划分为训练集和测试集。
• 参数说明：
  • X：特征数据。
  • y：目标标签。
  • test\_size：测试集比例（默认 20%）。
  • random\_state：随机种子，确保结果可复现 。
• 实现逻辑：
  • 使用 np.random.permutation 打乱数据索引。
  • 按比例划分测试集和训练集。

m = X.shape[0]                              # 获取数据集的大小 
permutation = np.random.permutation(m)      # 随机生成打乱的数组 对应为打乱的索引
test_size = int(m * test_size)              # 计算测试集的大小 
test_indices = permutation[:test_size]      # 取test_size个打乱的索引
train_indices = permutation[test_size:]     # 取后面所有索引作为训练集    

• 关键步骤：
  • X.shape[0]：获取样本总数。
  • permutation：生成随机索引。
  • test\_indices：前 test\_size 个索引作为测试集。
  • train\_indices：剩余索引作为训练集。

X_train = X[train_indices] 
X_test = X[test_indices] 
y_train = y[train_indices] 
y_test = y[test_indices] 
 
return X_train, X_test, y_train, y_test 

• 输出：返回划分后的训练集和测试集。

---

4. 贝叶斯分类器的预测函数

def predict_bayes(x, means, variances, priors): 
    posteriors = [] 
    for i in range(len(means)): 
        likelihood = np.prod(gaussian_pdf(x, means[i], np.sqrt(variances[i])))      
        posterior = likelihood * priors[i]                                          
        posteriors.append(posterior)                                                
    return np.argmax(posteriors) 

• 功能：基于朴素贝叶斯算法预测样本类别。
• 步骤解析：
  1. 似然计算：对每个特征计算高斯概率密度，并通过 np.prod 连乘得到联合概率（假设特征条件独立）。
  2. 后验概率：似然乘以先验概率 priors[i]。
  3. 分类决策：选择后验概率最大的类别作为预测结果（np.argmax）。

---

5. 生成合成数据集

X, y = make_classification(n_samples=1500, n_features=2, 
                            n_informative=2, n_redundant=0,  
                            n_clusters_per_class=1, random_state=6) 

• 功能：生成一个二维二分类数据集。
• 参数解释：
  • n\_samples=1500：生成 1500 个样本。
  • n\_features=2：每个样本有 2 个特征（x1, x2）。
  • n\_informative=2：两个特征均为信息性特征（用于分类）。
  • n\_redundant=0：无冗余特征。
  • n\_clusters\_per\_class=1：每个类别有 1 个聚类中心。
  • random\_state=6：确保数据生成可复现 。

---

6. 数据集划分

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2)

• 作用：将数据集按 80%/20% 划分为训练集和测试集。

---

7. 计算类别均值和方差

unique_classes = np.unique(y_train) 

means = []          
variances = []      
for i in unique_classes: 
    X_train_class_i = X_train[y_train == i]                 
    mean_class_i = np.mean(X_train_class_i, axis=0)         
    variance_class_i = np.var(X_train_class_i, axis=0)     
    means.append(mean_class_i) 
    variances.append(variance_class_i) 
 
means = np.array(means) 
variances = np.array(variances) 

• 功能：对每个类别计算特征的均值和方差。
• 关键点：
  • np.unique(y\_train)：获取训练集中所有类别标签。
  • X\_train[y\_train == i]：筛选当前类别的样本。
  • np.mean 和 np.var：计算均值和方差。

---

8. 计算先验概率

priors = [np.mean(y_train == i) for i in np.unique(y_train)] 

• 功能：计算每个类别的先验概率 $ P(Y) $。
• 实现原理：

对于布尔数组 y\_train == i，np.mean 返回 True（即类别 i 的样本）的比例。

9. 预测与评估

y_pred = [predict_bayes(x, means, variances, priors) for x in X_test] 
correct = np.sum(y_pred == y_test) / len(y_test)                            
print("Accuracy: {:.2f}%".format(correct * 100)) 

• 功能：
  • 对测试集逐样本预测类别。
  • 计算准确率：预测正确的样本数占总样本数的比例。

---

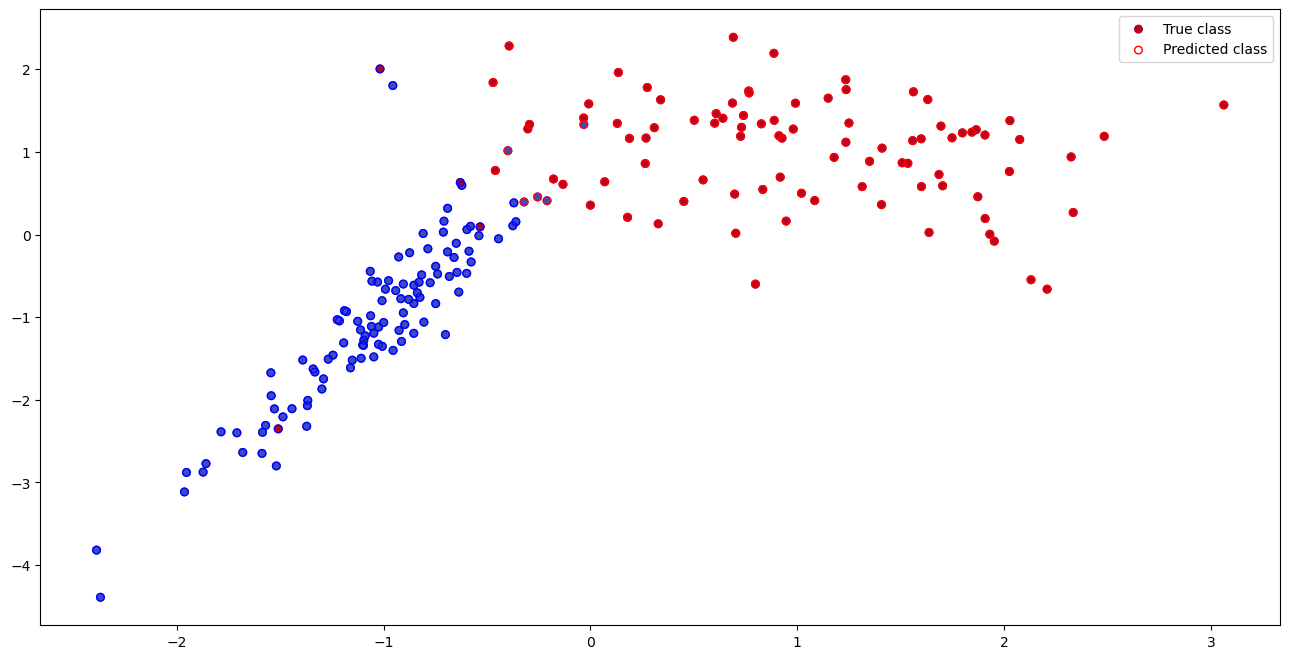
10. 可视化结果

plt.figure(figsize=(16, 8))
scatter_true = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test,  
                           s=30, cmap='coolwarm',label='True class') 
scatter_pred = plt.scatter(X_test[:, 0], X_test[:, 1], s=30,  
                           facecolors='none',  
                           edgecolors=np.array(['b', 'r'])[y_pred], 
                           label = 'Predicted class') 
plt.legend(handles=[scatter_true, scatter_pred]) 
plt.show()

• 功能：可视化测试集的真实标签和预测结果。
• 图形说明：
  • c=y\_test：颜色表示真实类别（红/蓝）。
  • edgecolors=np.array(['b', 'r'])[y\_pred]：边缘颜色表示预测类别。
  • facecolors='none'：仅显示边缘，便于对比预测与真实标签。

---

关键知识点总结

1. 朴素贝叶斯假设：特征之间条件独立，通过连乘计算联合概率 。
2. 高斯分布建模：假设每个特征在给定类别下服从正态分布。
3. 先验概率估计：通过训练集中类别的频率计算 $ P(Y) $。
4. 决策规则：最大化后验概率 $ P(Y|X) \propto P(X|Y)P(Y) $。

---

核函数估计概率密度函数的朴素贝叶斯

1. predict_bayes 函数：基于损失矩阵的贝叶斯决策

def predict_bayes(x, parzen_estimations, priors, loss_matrix): 
    expected_losses = []                                        # 初始化期望损失列表 
    for j in range(len(parzen_estimations)): 
        expected_loss = 0                                       # 初始化期望损失 
        for i in range(len(parzen_estimations)): 
            posterior = priors[i] * parzen_estimations[i]       # 计算后验概率     
            expected_loss += loss_matrix[i][j] * posterior      # 计算期望损失 
        expected_losses.append(expected_loss)                   # 将期望损失添加到列表中 
    return np.argmin(expected_losses, axis=0)                   # 返回期望损失最小的类别作为预测结果

• 功能：根据期望损失最小化原则，将输入样本 x 分类到某个类别。
• 关键步骤解析：
  1. 后验概率计算：

     posterior = priors[i] * parzen_estimations[i]

     • 公式：
  • 理论依据：贝叶斯定理 $ P(Y|X) = \frac{P(Y) \cdot P(X|Y)}{P(X)} $，分母 $ P(X) $ 对所有类别相同，可忽略 。

1. 期望损失计算：

   expected_loss += loss_matrix[i][j] * posterior

   • 公式：

• 理论依据：贝叶斯决策的目标是最小化条件风险（即期望损失），而非单纯最大化后验概率 。

2. 决策规则：

   return np.argmin(expected_losses, axis=0)

   • 解释：选择期望损失最小的类别 j 作为预测结果，而非直接选择后验概率最大的类别。
   • 对比普通贝叶斯：普通朴素贝叶斯仅比较后验概率（即损失矩阵为单位矩阵时的情况），而此代码通过自定义 loss\_matrix 实现风险敏感决策 。

---

2. Parzen窗口估计：非参数概率密度估计

def parzen_window_estimation(x, data, h=1, window_func=squ_window): 
    N, d = data.shape                           # 获取数据的数量和维度
    k_n = window_func(cdist(x, data) / h)       # 计算每个样本到x的距离并应用窗口函数限制权重
    return np.sum(k_n, axis=1) / (N * h**d)     # 返回Parzen窗口估计的结果 shape=[N, ] h是窗大小

• 功能：通过Parzen窗口法估计样本 x 的概率密度。
• 关键步骤解析：
  1. 距离计算：

     cdist(x, data) / h

     • 作用：计算测试样本 x 与所有训练样本 data 的欧氏距离，并除以带宽 h 进行归一化。
     • 理论依据：Parzen窗口是一种非参数密度估计方法，通过核函数（窗口函数）加权邻域内的样本点 。
  2. 窗口函数应用：

     window_func(...)

     • 窗口函数类型：
       • 方窗（squ\_window）：仅统计距离在 [-h/2, h/2] 内的样本。
       • 正态窗（nor\_window）：使用高斯分布权重（权重随距离指数衰减）。
       • 指数窗（exp\_window）：权重随距离线性衰减。
       • 三角窗（tri\_window）：权重随距离线性衰减至零。
     • 理论依据：不同窗口函数对密度估计的平滑性有影响，正态窗适合连续分布，方窗适合离散分布 。
  3. 密度估计值：

     np.sum(...) / (N * h**d)

     • 公式：
  • 理论依据：Parzen窗口通过核密度估计逼近真实分布，无需假设数据服从特定分布 。

---

3. 代码整体流程与贝叶斯决策的关系

1. 训练阶段：
   • 对每个类别 i，使用训练数据 X\_train[y\_train == i] 计算 Parzen 窗口密度估计 parzen\_estimations[i]。
   • 计算每个类别的先验概率 priors[i] = P(Y=i)。
2. 预测阶段：
   • 对每个测试样本 x：
     • 使用 Parzen 窗口法计算其在每个类别下的概率密度 parzen\_estimations。
     • 结合先验概率和损失矩阵，计算每个可能决策的期望损失。
     • 选择期望损失最小的类别作为预测结果。
3. 与普通朴素贝叶斯的区别：
   • 普通朴素贝叶斯：假设特征服从特定分布（如高斯分布），且特征条件独立，直接计算后验概率。
   • 本代码实现：
     • 使用非参数方法（Parzen窗口）估计概率密度，无需假设分布形式。
     • 引入损失矩阵，允许自定义误分类代价（如医疗诊断中误诊癌症的代价更高）。

---

4. 关键参数的作用

• 带宽 **h**：
  • h 越大，密度估计越平滑（可能欠拟合），h 越小，密度估计越尖锐（可能过拟合）。
• 窗口函数：
  • 方窗（squ\_window）适合离散分布，正态窗（nor\_window）适合连续分布。
• 损失矩阵 **loss\_matrix**：
  • 单位矩阵（[[0,1],[1,0]]）对应最小错误率决策，非单位矩阵对应最小风险决策 。

---

5. 示例说明

假设 loss\_matrix = [[0, 2], [1, 0]]：

• 将实际类别为 0 的样本误判为 1 的代价是 2，而将实际类别为 1 的样本误判为 0 的代价是 1。
• 分类器会更倾向于避免将类别 0 误判为 1，从而在代价敏感场景下优化决策 。

---

总结

• 核心思想：通过非参数密度估计（Parzen窗口）和风险最小化（损失矩阵）实现灵活的贝叶斯决策。
• 适用场景：
  • 数据分布未知或非高斯分布。
  • 不同类别的误分类代价不一致（如医疗、金融风控）。
• 改进方向：
  • 使用交叉验证选择最优带宽 h。
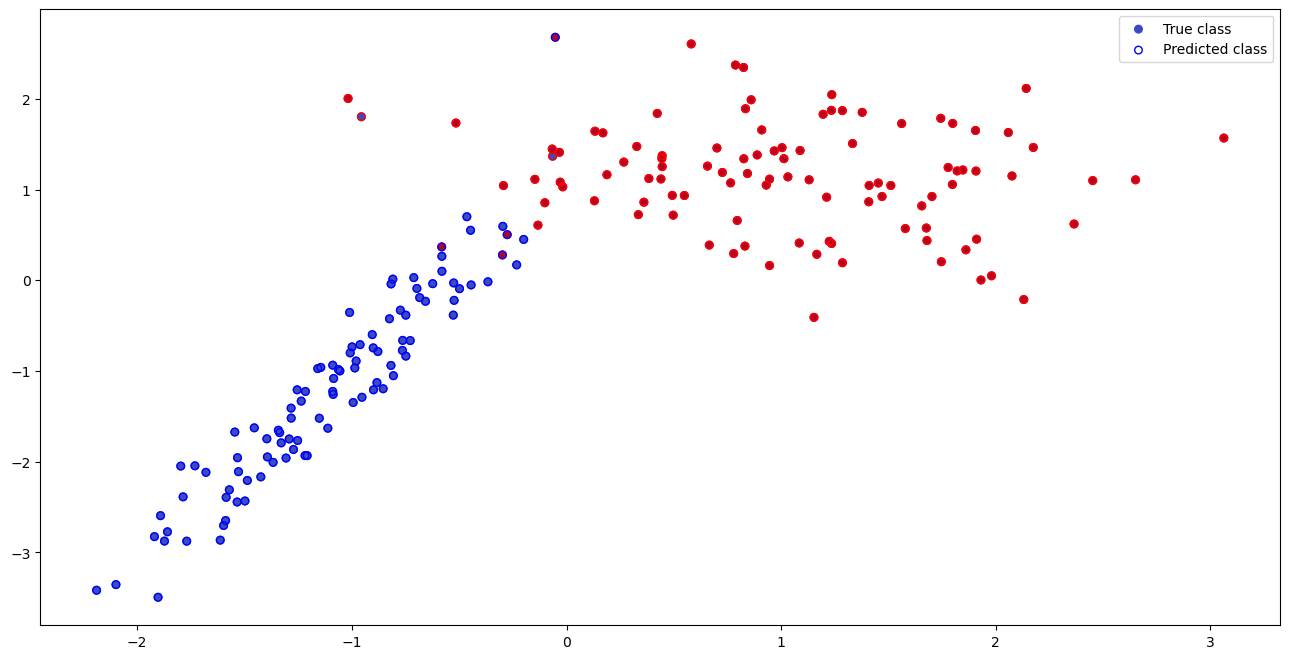
  • 替换更复杂的核函数（如高斯混合核）。

➡️ 通过加窗以及损失矩阵补偿错误判断，可以发现对于同一个数据在分类的正确性上有一定的增强；