通信原理——MATLAB仿真

Analog Modulation 模拟调制

幅度调制 —— AM

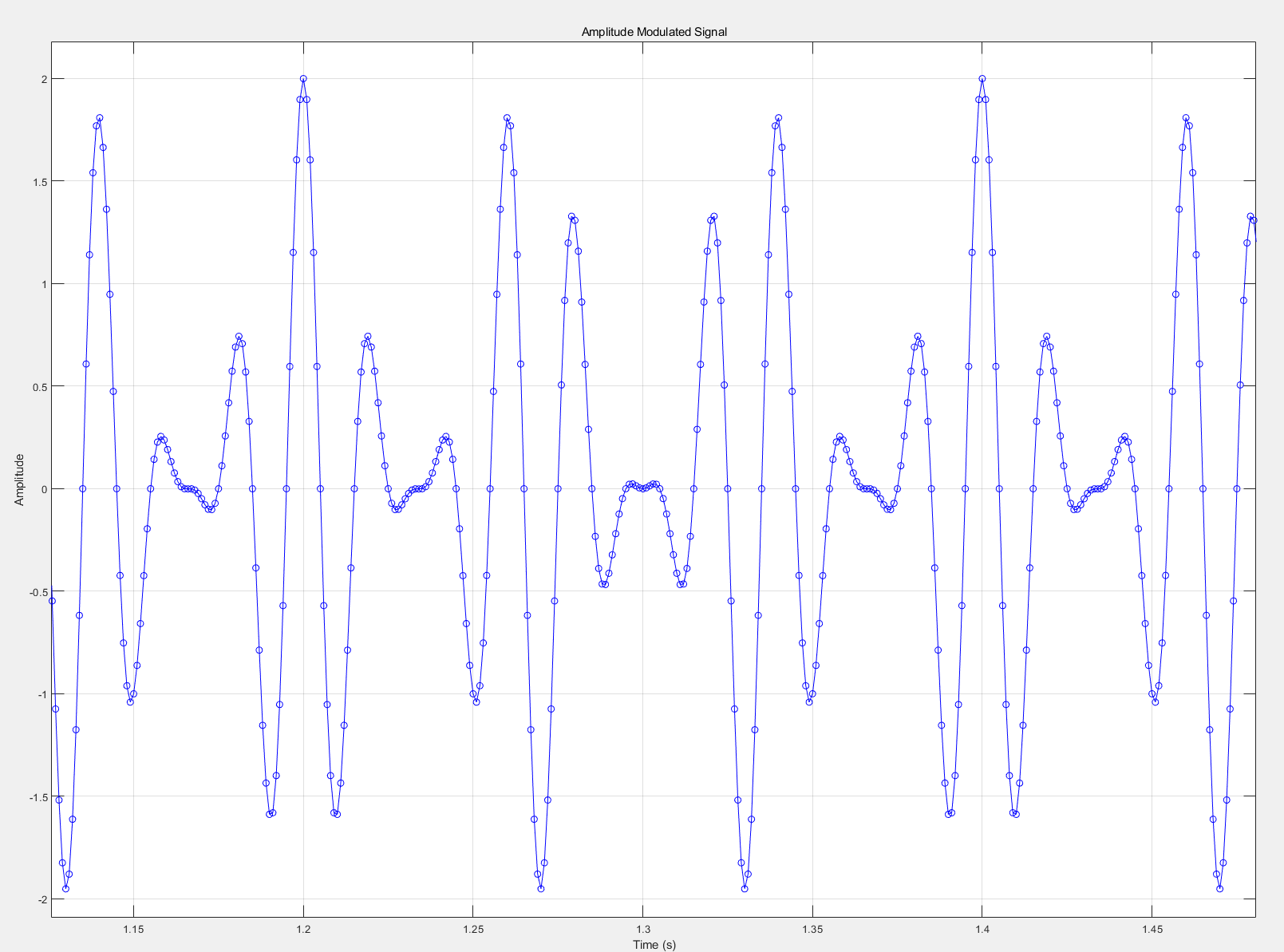
image
上图为MATLAB仿真的AM波形，代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
f0 = 50;    % Carrier Freq: 50Hz
fm = 15;    % Message Freq: 24Hz

num_points = 4096;
t0 = 1 / f0;
t = 1:t0:num_points*t0;

Am = 1;     % Amplitude of Message Signal
Ac = 1;     % Amplitude of Carrier Signal

mt = Am * cos(2 * pi * fm * t);
st = Ac * (1 + mt) .* cos(2 * pi * f0 * t);

figure;
plot(t, st, '-ob');
xlabel('Time (s)');
ylabel('Amplitude');
title('Amplitude Modulated Signal');
grid on;

这里我们设置信息频率与载波频率分别为 $15Hz, 50Hz$，可以自行尝试不同的频率选择，不同的频率得到的调制信号不相同。

AM的调制公式如下：

$$S(t) = A_{c} (1 + m(t)) \cos{2\pi f_{c}t}$$

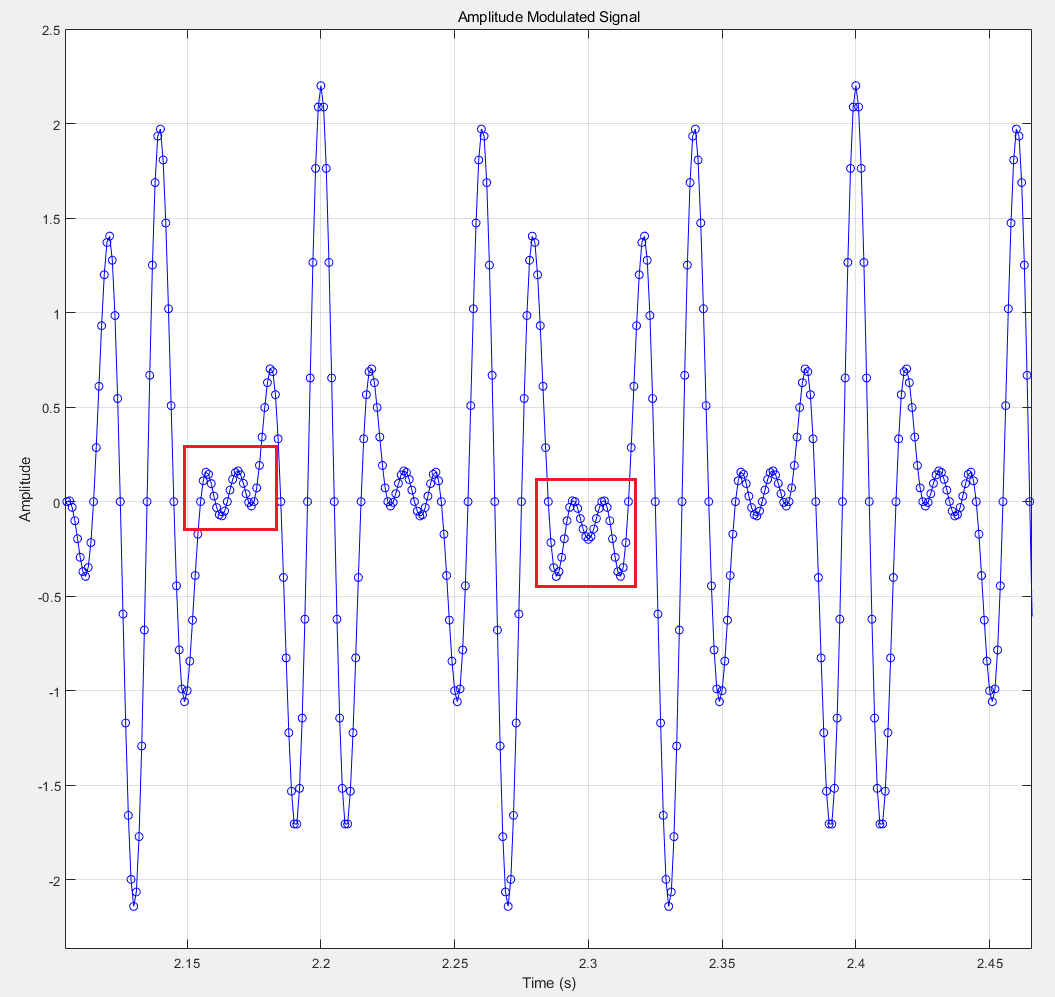
如果信息 $m(t)$ 的幅度超过 $1$，则会出现过调制的问题，详见下：

image
对比两幅图片可以明显的发现红色方框处出现了过调制的问题。

下面计算AM调制的功率、实际功率、调制效率以及功率谱： 

1
2
3
4
5
6
beta = (max(st) - Ac) / Ac;         % Modulation Index
mu = Am / Ac;                       % Modulation Depth
Ps = (1/2) * Ac^2 * mean(1 + mt.^2);% Power of the Modulated Signal
Pc = (1/2) * Ac^2;                  % Power of the Carrier Signal
Pm = (1/2) * Ac^2 * mean(mt.^2);    % Power of the Message Signal
efficiency = (Pm / Ps) * 100;       % Efficiency of the Modulated Signal
1
2
3
4
5
6
=== AM信号功率分析 ===
调制深度 (μ): 1.200
载波功率: 0.500 W
理论总功率: 0.860 W
实际总功率: 0.360 W
调制效率: 41.84%

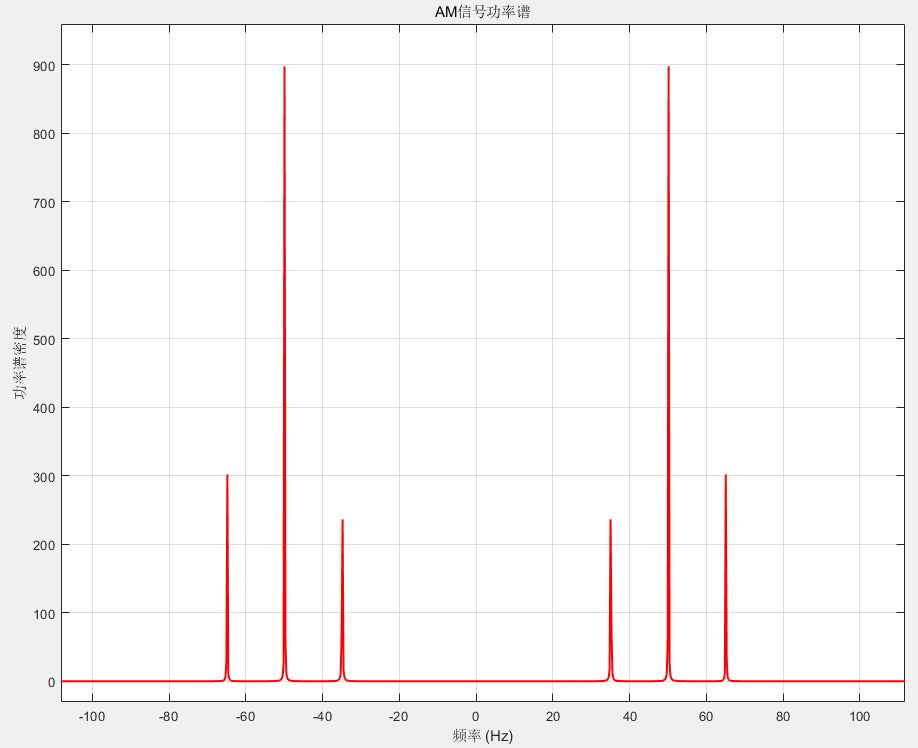
功率谱如下：

image

DSB-SC —— 双边带抑制载波

是一种线性幅度调制方式，属于 AM 调制家族，但与常规 AM 不同，它不发送载波分量，仅发送上下两个边带。

从公式上观察，DSB-SC的调制信号没有直流偏置的存在：

$$s_{DSB-SC}(t) = m(t) \cos(2 \pi f_c t)$$

对应的频域公式为：

$$S_{DSB-SC}(f) = \frac{1}{2} \left[ M(f - f_c) + M(f + f_c) \right]$$

这样的好处是，节省了载波的功率，从某种意义上来说等价于过调制的存在。

但是由于过调制，导致DSB-SC的解调不能像AM一样通过简单的包络检波实现，因为此时的包络与调制信号不成正比；而是需要使用相干解调，这就需要接收端产生本振，节省的载波能量以另一种形式消耗了。

image

实现代码如下： 

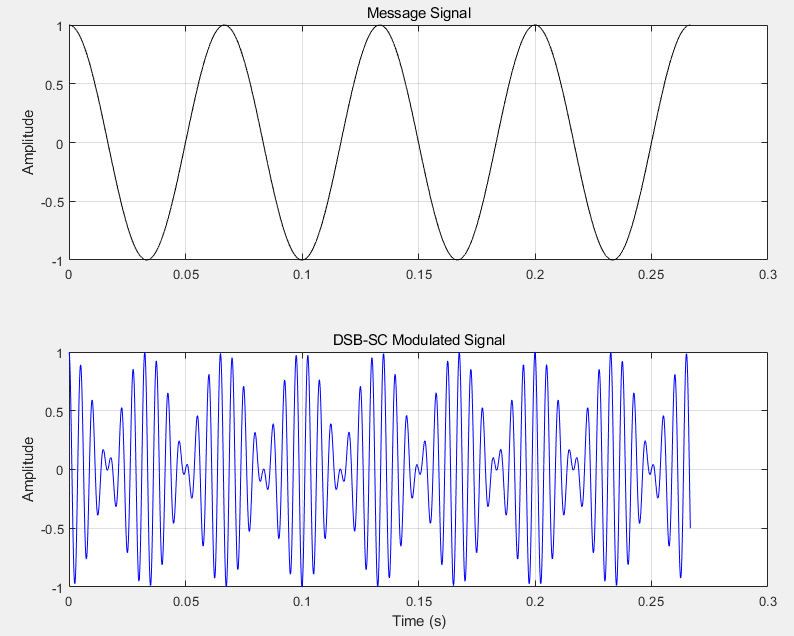
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
num_points = 16384;

Am = 1;
fm = 15;
Tm = 1 / fm;
t = linspace(0, 4 * Tm, num_points);

mt = Am * cos(2 * pi * fm * t);

fc = 200;
Ac = 1;
st = Ac * mt .* cos(2 * pi * fc * t);

figure;
subplot(2, 1, 1);
plot(t, mt, '-k');
ylabel('Amplitude');
title('Message Signal');
grid on;

subplot(2, 1, 2);
plot(t, st, '-b');
xlabel('Time (s)');
ylabel('Amplitude');
title('DSB-SC Modulated Signal');
grid on;

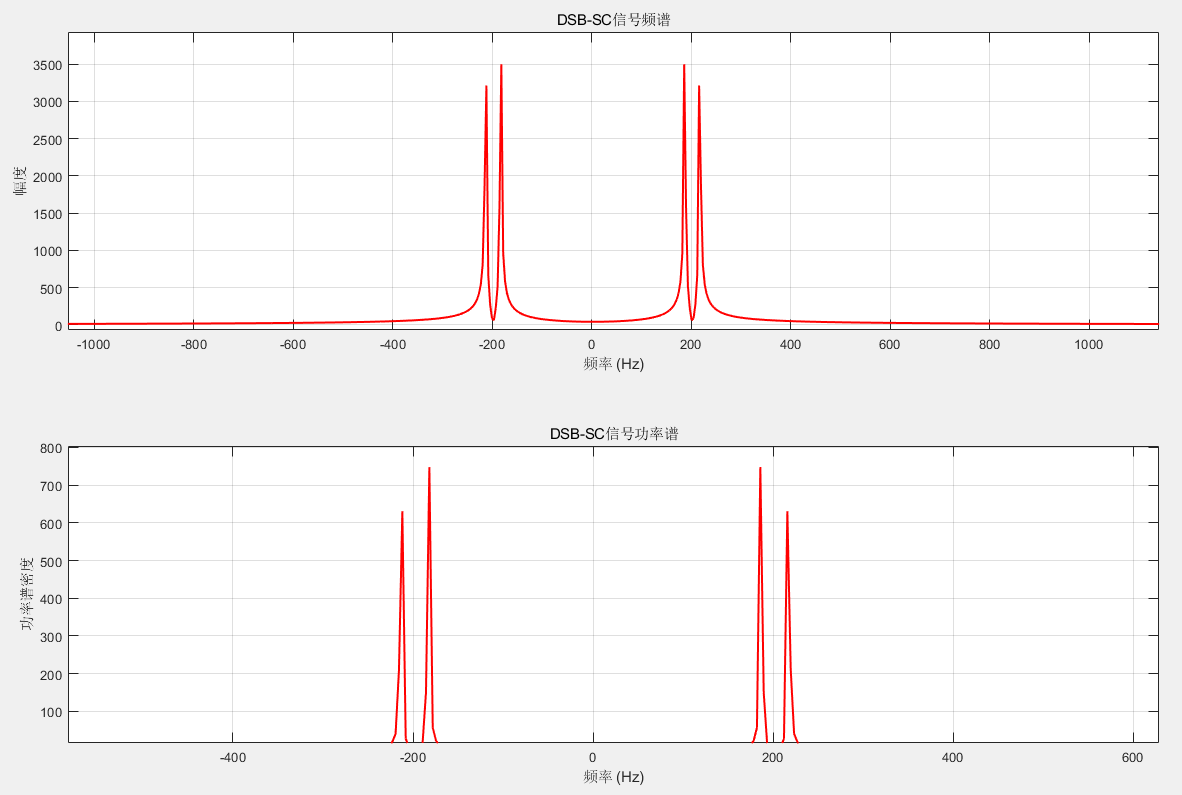
对应的频谱和功率谱如下：

image

纵轴的数值异常是由于没有功率归一化导致的，具体脚本如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
num_spectrum = num_points;

fs = num_points / (4 * Tm);
f = linspace(-fs/2, fs/2, num_spectrum);
St_fft = fftshift(fft(st));

figure;
subplot(2, 1, 1);
plot(f, abs(St_fft), 'r-', 'LineWidth', 1.5);
xlabel('频率 (Hz)');
ylabel('幅度');
title('DSB-SC信号频谱');
grid on;

subplot(2, 1, 2);
plot(f, abs(St_fft).^2/length(st), 'r-', 'LineWidth', 1.5);
xlabel('频率 (Hz)');
ylabel('功率谱密度');
title('DSB-SC信号功率谱');
grid on;

通过对调制信号和已调信号的功率分析，发现所有的功率全部用于调制信号并发送，调制效率理论上是100%！ 

1
2
3
4
5
6
7
8
9
10
11
12
BW_before = fm;
BW_after = 2 * fm;
Ps = (1/2) * Ac^2 * mean(mt.^2);    % Power of the Modulated Signal
Pc = 0;                              % Power of the Carrier Signal
Pm = (1/2) * Ac^2 * mean(mt.^2);    % Power of the Message Signal
efficiency = (Pm / Ps) * 100;       % Efficiency of the Modulated

fprintf('=== DSB-SC信号功率分析 ===\n');
fprintf('载波功率: %.3f W\n', Pc);
fprintf('理论总功率: %.3f W\n', Ps);
fprintf('实际总功率: %.3f W\n', Pm);
fprintf('调制效率: %.2f%%\n', efficiency);

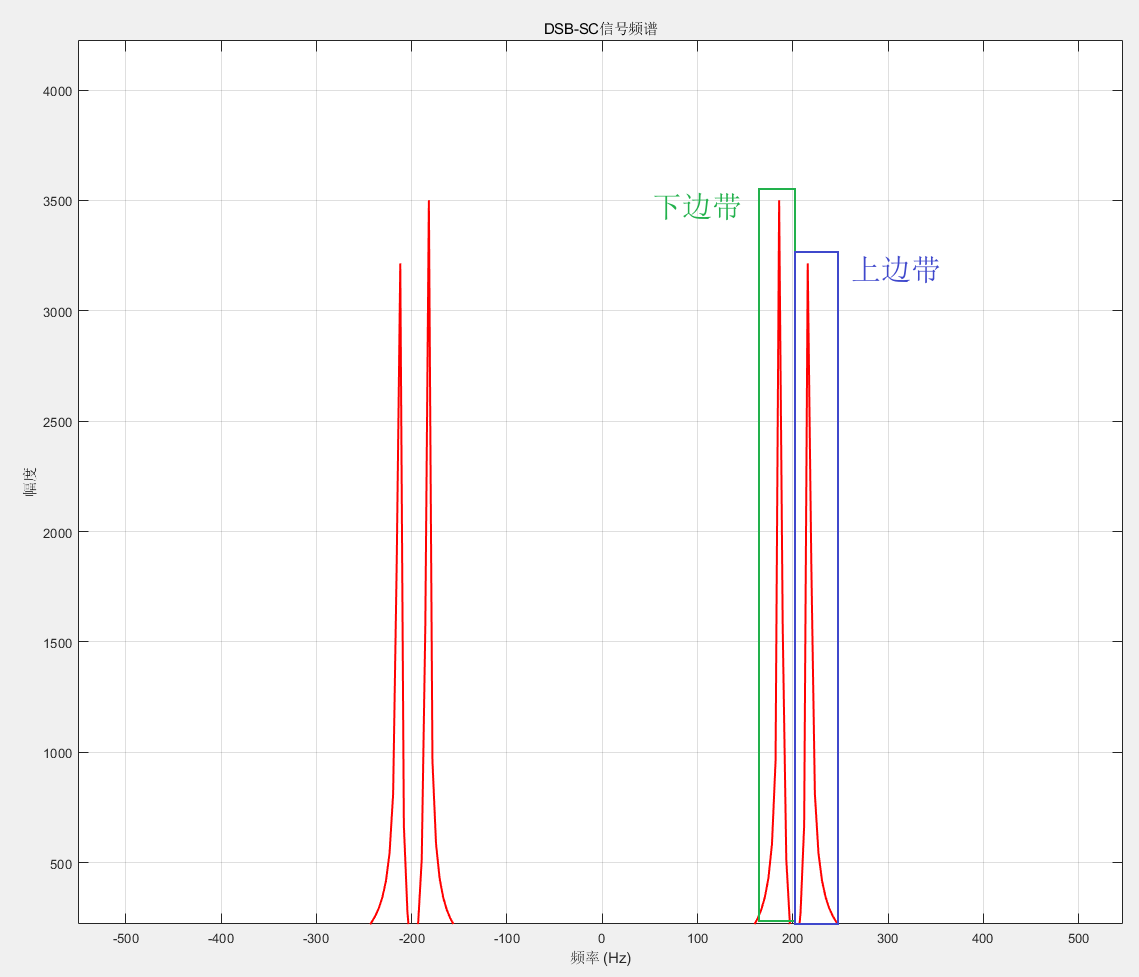
SSB-SC —— 单边带抑制载波

基本原理与DSB-SC相同，只不过DSB-SC调制完后包含有两个边带，上边带（USB）和下边带（LSB），而SSB-SC就是只保留其中一个边带，节省带宽。

原来的DSB-SC频谱如下：

image

如何实现SSB-SC呢？我们一般从频域入手：

  1. 滤波法（最直观）
  • 先生成 DSB-SC 信号
  • 用理想边带滤波器滤除一个边带
  • ⚠️ 缺点：当 $f_m$很小（如语音信号 $300Hz$）而 $f_c$很大（如 $1MHz$），边带靠得太近，物理滤波器难以实现陡峭截止
  1. 相移法（Hilbert 变换法）
    利用 Hilbert 变换构造解析信号：
    $$s_{SSB}(t)=\frac{1}{2}[m(t)cos(2πf_c t) ∓ \hat{m}(t)sin(2πf_c t)]$$
  • 上边带（USB）取 “−”
  • 下边带（LSB）取 “+”
  • $\hat{m}(t)$是 $m(t)$的 $Hilbert$变换（相移 $-90°$）

📌 优点：无需陡峭滤波器，适合宽带/低频基带信号

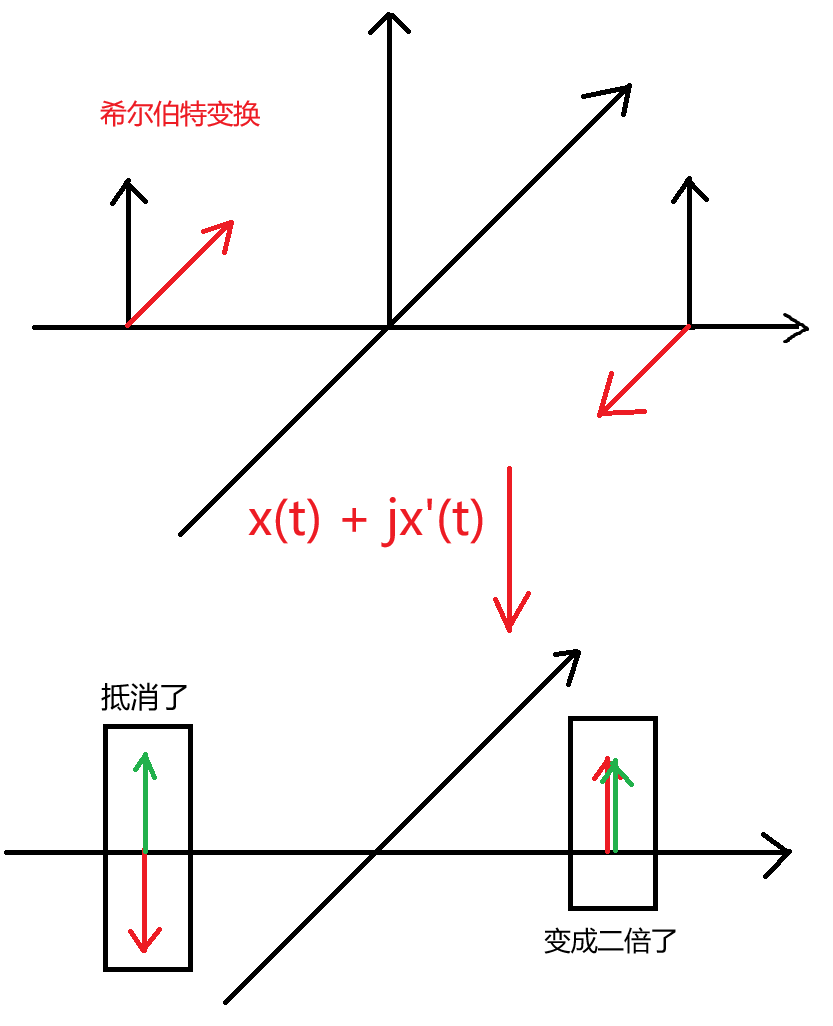
知识点补充——希尔伯特变换得到解析信号：

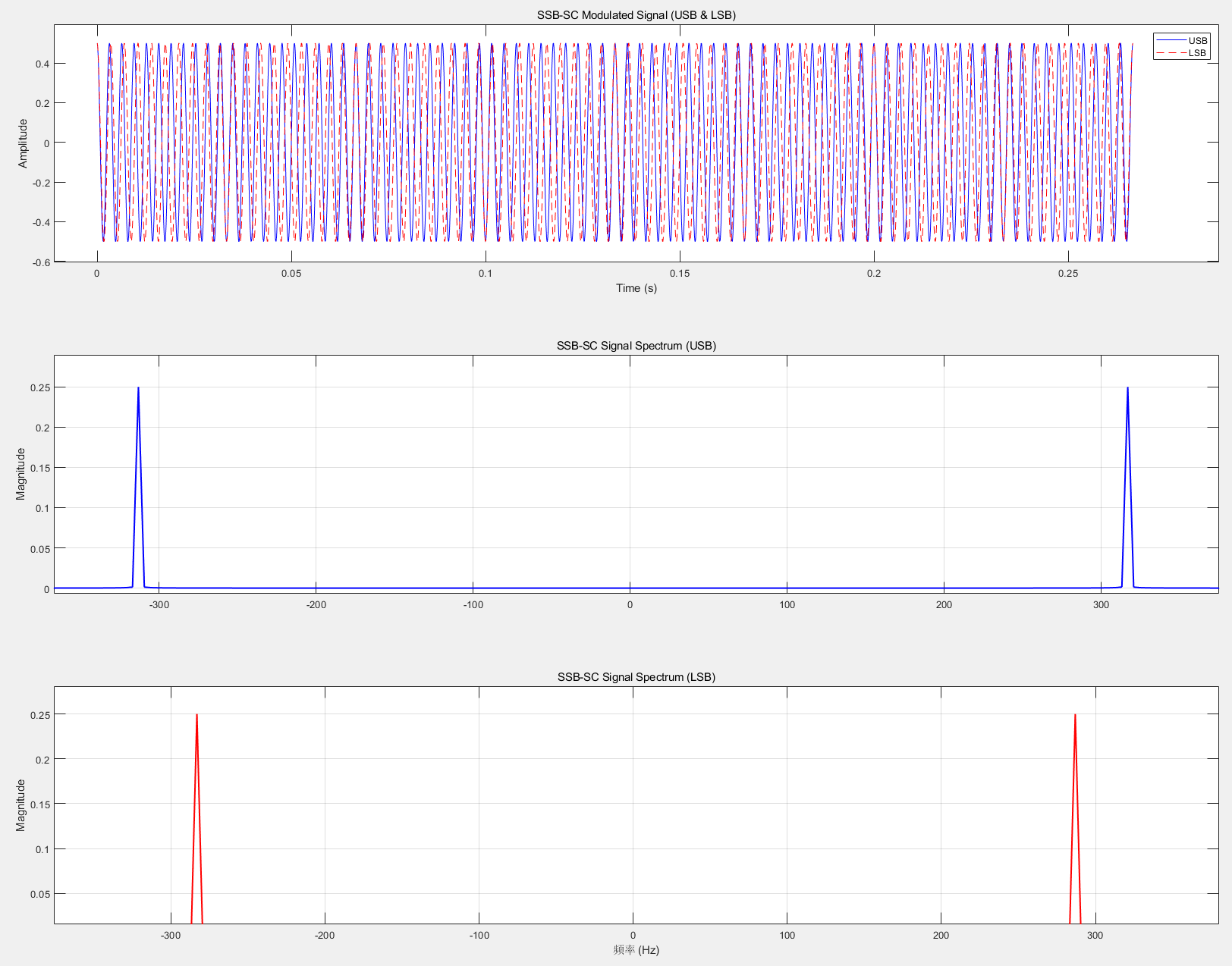
image

通过上述可以得到单边带信号；

image

上图是基于相移法得到的单边带调制，实现代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
num_points = 16384;

Am = 1;
fm = 15;
Tm = 1 / fm;
t = linspace(0, 4 * Tm, num_points);
mt = Am * cos(2 * pi * fm * t);

mt_hilbert = hilbert(mt);
mt_hat = imag(mt_hilbert);  % Hilbert Transform

fc = 300;
Ac = 1;
st_USB = (1 / 2) * Ac * (mt .* cos(2 * pi * fc * t) - mt_hat .* sin(2 * pi * fc * t));
st_LSB = (1 / 2) * Ac * (mt .* cos(2 * pi * fc * t) + mt_hat .* sin(2 * pi * fc * t));

figure;
subplot(3, 1, 1);
plot(t, st_USB, '-b');
hold on;
plot(t, st_LSB, '--r');
xlabel('Time (s)');
ylabel('Amplitude');
title('SSB-SC Modulated Signal (USB & LSB)');
legend('USB', 'LSB');

num_spectrum = num_points;
fs = num_spectrum / (4 * Tm);
f = linspace(-fs/2, fs/2, num_spectrum);
St_USB_fft = fftshift(fft(st_USB));
St_LSB_fft = fftshift(fft(st_LSB));

subplot(3, 1, 2);
plot(f, abs(St_USB_fft) / num_spectrum, 'b-', 'LineWidth', 1.5);
ylabel('Magnitude');
title('SSB-SC Signal Spectrum (USB)');
grid on;

subplot(3, 1, 3);
plot(f, abs(St_LSB_fft) / num_spectrum, 'r-', 'LineWidth', 1.5);
xlabel('频率 (Hz)');
ylabel('Magnitude');
title('SSB-SC Signal Spectrum (LSB)');
grid on;

角度调制 —— FM

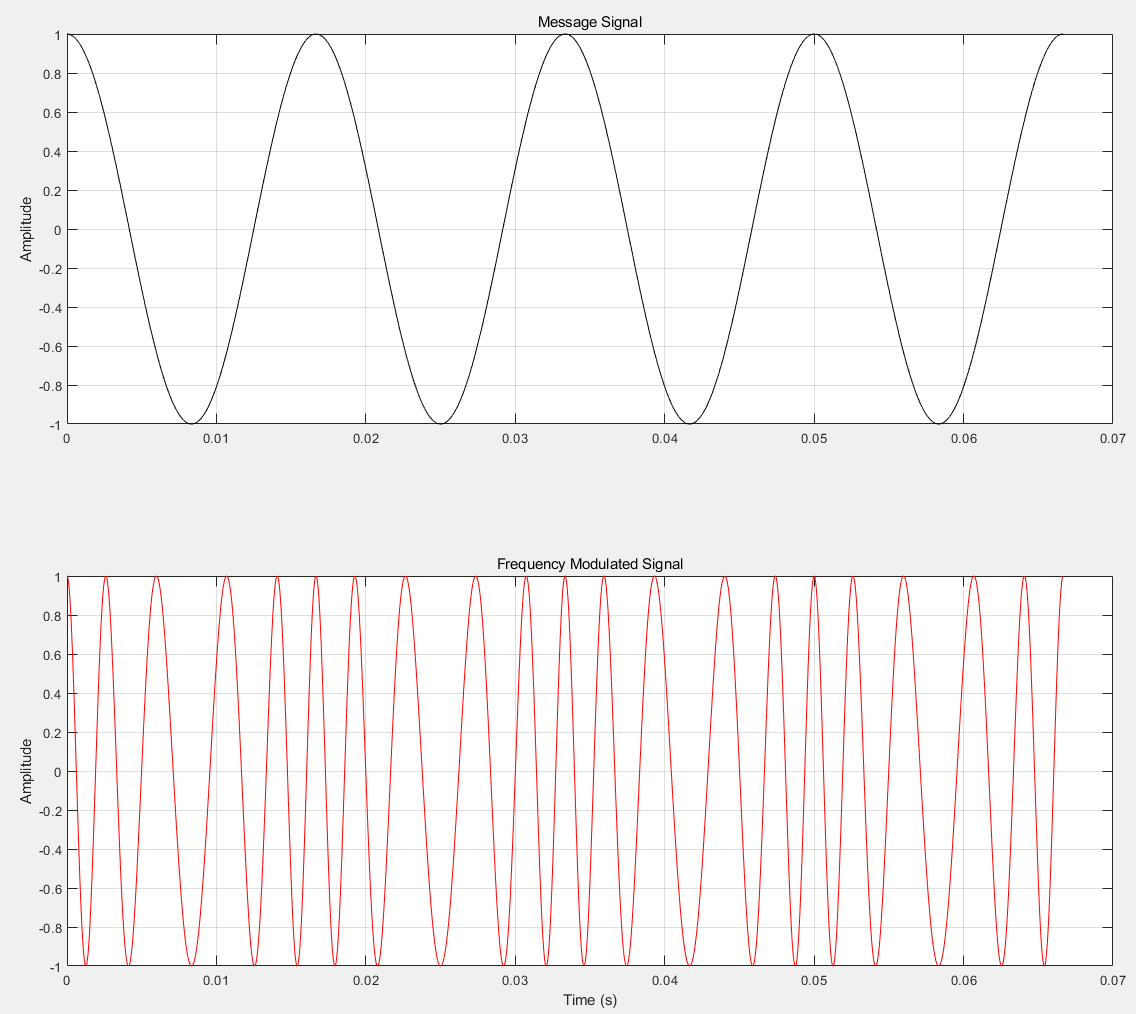
image 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
num_points = 16384;

fm = 60;
Tm = 1 / fm;
t = linspace(0, 4 * Tm, num_points);

Am = 1;
Kf = 100;        % Hz/Volt 每伏特对应多少的频率偏移
mt = Am * cos(2 * pi * fm * t);

fc = 300;
Ac = 1;

integral_mt = cumtrapz(t, mt);
phi = 2 * pi * fc * t + 2 * pi * Kf * integral_mt;  % 相位 以PM的方式调制FM
st = Ac * cos(phi);

figure;
subplot(2, 1, 1);
plot(t, mt, '-k');
ylabel('Amplitude');
title('Message Signal');
grid on;

subplot(2, 1, 2);
plot(t, st, '-r');
xlabel('Time (s)');
ylabel('Amplitude');
title('Frequency Modulated Signal');
grid on;

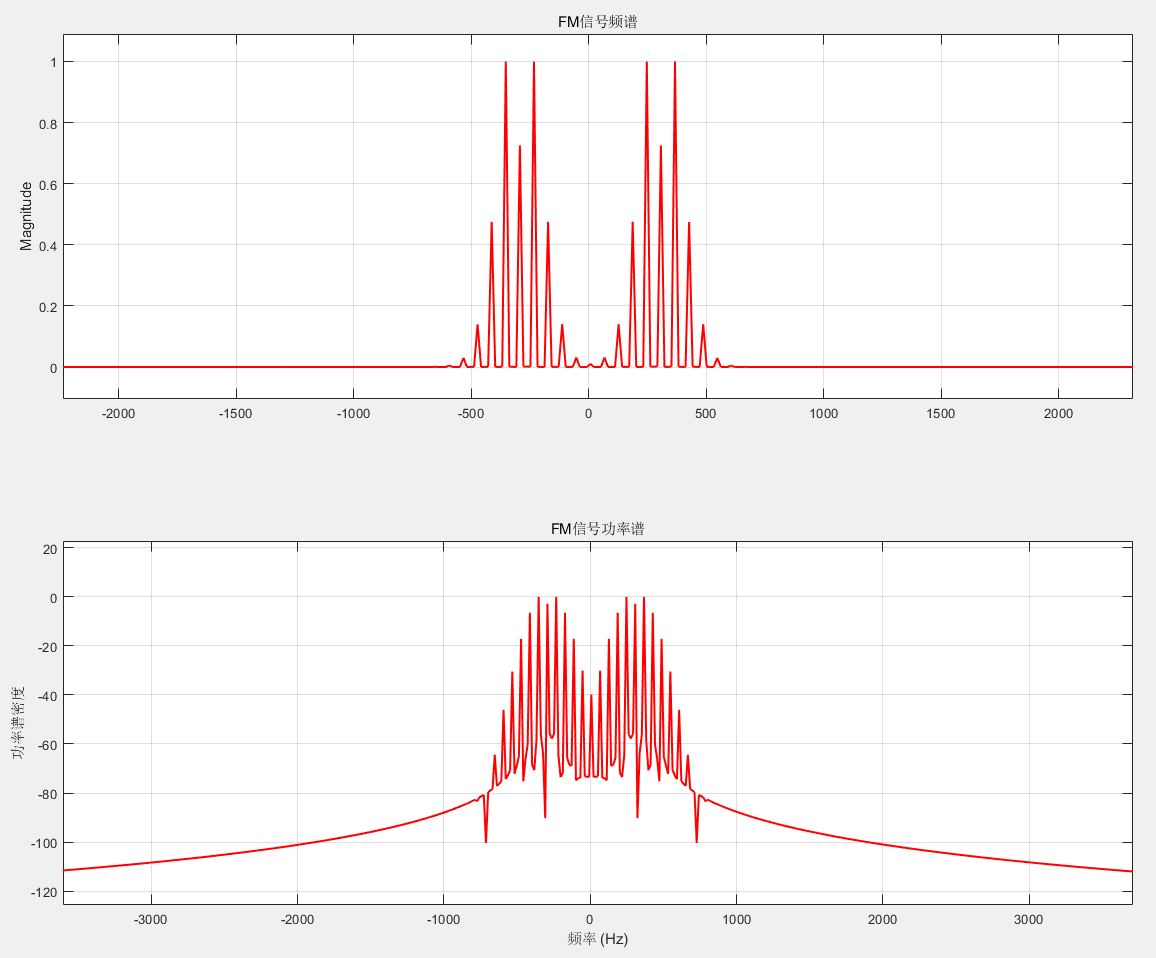
计算功率谱（频谱）可以看到有多个边带：

image 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
num_spectrum = num_points;
fs = num_spectrum / (4 * Tm);
f = linspace(-fs/2, fs/2, num_spectrum);
St_fft = fftshift(fft(st));

figure;
subplot(2, 1, 1);
plot(f, abs(St_fft)/max(abs(St_fft)), 'r-', 'LineWidth', 1.5);
ylabel('Magnitude');
title('FM信号频谱');
grid on;

subplot(2, 1, 2);
plot(f, 20*log10(abs(St_fft)/max(abs(St_fft))), 'r-', 'LineWidth', 1.5);
xlabel('频率 (Hz)');
ylabel('功率谱密度');
title('FM信号功率谱');
grid on;

这是因为FM 是非线性调制，会导致在频谱上出现频偏，导致带宽的扩展以及无限多的频谱！

与 AM（幅度调制）不同，FM 是一种非线性调制方式，其已调信号可以展开为一个无穷级数，包含载波和无数对边频分量。

对于单音 FM 信号：

$$s(t) = A_c \cos{(2 \pi f_c t + \beta \sin{2 \pi f_m t})}$$

对于上述FM调制信号来说，其傅里叶展开为无穷级数：

$$s(t) = A_c \sum_{n=-\infty}^{\infty} J_n(\beta) \cos\left[2\pi (f_c + n f_m)t\right]$$

其中：

  • $Jn(β)$：第$n$阶第一类贝塞尔函数（Bessel function）
  • $β$：调制指数（代码中约为 0.67）
  • $fm$：调制信号频率（30 Hz）
  • $fc$：载波频率（100 Hz）

因为参数的设定（1000Hz采样率，4096个点，频谱分辨率0.24Hz），因此可以清晰的看到不同的峰值。

  • $Kf=20Hz/V, Am=1⇒Δf=20Hz$
  • $β=\frac{fm}{Δf}=\frac{30}{20}≈0.67$

所以计算第一类贝塞尔曲线函数可得：

  • $J0(0.67)≈0.8$→ 主载波较强
  • $J1(0.67)≈0.32$→ 第一阶边带明显
  • $J2(0.67)≈0.06$→ 第二阶较弱但仍可见
  • 更高阶迅速衰减

因此设置不同的参数可以有很明显的频谱差异。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
% 最大频偏 (Maximum Frequency Deviation)
delta_f = Kf * Am;  % Hz

% 最大相偏 (Maximum Phase Deviation)
delta_phi = delta_f / fm;  % rad

% 调频指数 (Modulation Index)
beta_fm = delta_f / fm;

% 带宽计算
% Carson带宽规则: BW = 2(Δf + fm)
BW_carson = 2 * (delta_f + fm);  % Hz

% 近似带宽 (当β > 1时)
if beta_fm > 1
    BW_approx = 2 * delta_f;  % 宽带FM
else
    BW_approx = 2 * fm;       % 窄带FM
end

% 瞬时频率计算
dt = t(2) - t(1);
inst_freq = fc + Kf * mt;  % 瞬时频率

% 功率计算
P_fm = mean(st.^2);         % FM信号功率
P_carrier = Ac^2 / 2;       % 理论载波功率

% 结果显示
fprintf('=== FM信号参数分析 ===\n');
fprintf('载波频率 (fc): %.1f Hz\n', fc);
fprintf('调制频率 (fm): %.1f Hz\n', fm);
fprintf('频率灵敏度 (Kf): %.1f Hz/V\n', Kf);
fprintf('调制信号幅度 (Am): %.1f V\n', Am);
fprintf('最大频偏 (Δf): %.1f Hz\n', delta_f);
fprintf('最大相偏 (Δφ): %.2f rad\n', delta_phi);
fprintf('调频指数 (β): %.2f\n', beta_fm);
fprintf('Carson带宽: %.1f Hz\n', BW_carson);
fprintf('近似带宽: %.1f Hz\n', BW_approx);
fprintf('信号功率: %.3f W\n', P_fm);
fprintf('理论功率: %.3f W\n', P_carrier);

if beta_fm > 1
    fprintf('调制类型: 宽带FM\n');
else
    fprintf('调制类型: 窄带FM\n');
end

相关的参数计算如上，本脚本的参数如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
=== FM信号参数分析 ===
载波频率 (fc): 300.0 Hz
调制频率 (fm): 60.0 Hz
频率灵敏度 (Kf): 100.0 Hz/V
调制信号幅度 (Am): 1.0 V
最大频偏 (Δf): 100.0 Hz
最大相偏 (Δφ): 1.67 rad
调频指数 (β): 1.67
Carson带宽: 320.0 Hz
近似带宽: 200.0 Hz
信号功率: 0.500 W
理论功率: 0.500 W
调制类型: 宽带FM